| boltz |
Boltzmann's constant (1.38062e-23 joules/degree kelvin) |
| const_c |
The speed of light (2.997925e8 meters/second) |
| const_e |
The base of natural logarithms (2.71828182844590452353) |
| echarge |
The charge on an electron (1.60219e-19 coulombs) |
| false |
False value (0) |
| const_j |
The square root of -1, can be expressed as (0,1) |
| kelvin |
Absolute 0 in Centigrade (-273.15 degrees) |
| no |
False value (0) |
| phi0 |
The flux quantum (Planck's constant over twice echarge) |
| phi0_2pi |
Value of the flux quantum normalized to 2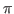
|
| pi |
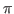 (3.14159265358979323846)
(3.14159265358979323846) |
| planck |
Planck's constant (6.62620e-34 joule-seconds) |
| true |
Truth value (1) |
| yes |
Truth value (1) |